In diesem Kapitel werden statistische Prognosemodelle für einzelne Länder entwickelt. Für alle zu untersuchenden Länder werden jeweils ARIMA und ETS Modelle spezifiziert . Für die umsatzstärkeren Länder Deutschland, Spanien und Italien werden ebenfalls DR Modelle entwickelt.
Um die Genauigkeit der Prognosen anschließend vergleichen und bewerten zu können, werden die Zeitreihen in Trainings- und Testdaten separiert. Für die Zeitreihen aller Länder sind Beobachtungen bis einschließlich April 2018 vorhanden. Die letzten vier92 Beobachtungen (Januar, Februar, März und April 2018) werden jeweils als Testdaten einbehalten und fließen nicht in die Spezifikation der Modelle ein.
Am Beispiel des Landes Spanien wird nun die Anpassung der ARIMA Modelle diskutiert . Wie in Kapitel 3.2 dargestellt, besteht die grundlegende Modellannahme der ARIMA Modelle in der Stationarität der vorliegenden Zeitreihe. Es wird demnach insbesondere Mittelwert- und Varianzstationarität gefordert. Im oberen Anteil der Abbildung 12 ist nochmals die originäre Zeitreihe der Verkäufe in Euro für Spanien dargestellt. Die Zeitreihe ist nicht mittelwertstationär, da sie einen positiven Trend verzeichnet. Das Kriterium der Varianzstabilität ist ebenfalls nicht erfüllt, da die Varianz der Zeitreihe mit steigender Dauer der Zeitreihe zunimmt. Wie in Abbildung 6 bzw. Abbildung 7 ersichtlich ist, treffen diese beiden Charakteristika auf die Zeitreihen aller 13 Länder zu. Varianzstabilität kann über geeignete mathematische Transformationen hergestellt werden. Die untere Zeitreihe aus Abbildung 12 resultiert aus der sogenannten Box-Cox Transformation93 mit dem Parameter λ = 0,6428.
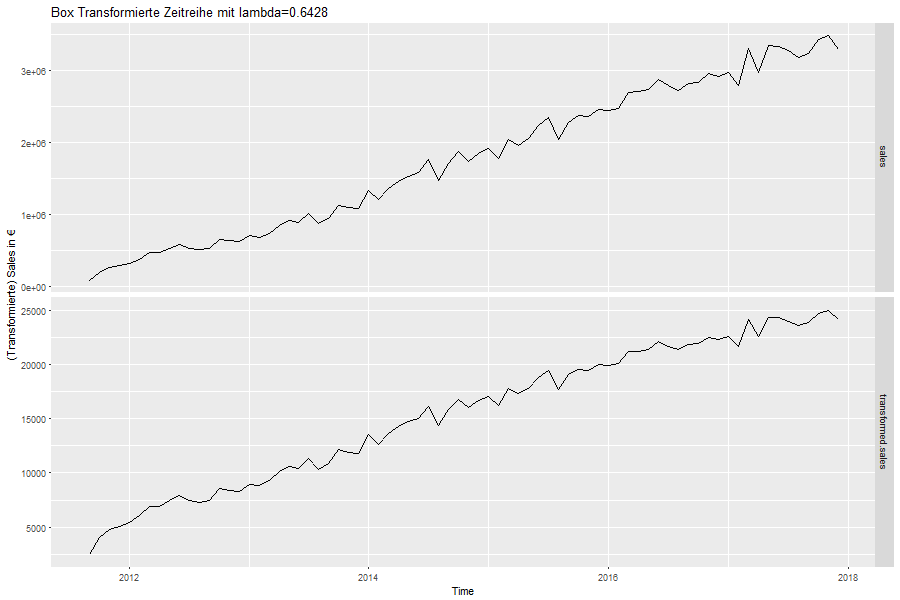
Die Box-Cox Transformation einer originären Zeitreihe yt ist durch folgende Abbildung definiert:
(4.4.1) wt (λ) = { 𝑦𝑡 λ − 1 (λ ≠ 0) 𝑙𝑛(λ) (λ = 0)
Die Bijektivität der Abbildung gewährleistet, dass die mit dem Arima Modell später prognostizierten wt+1. . . wt+h auf die Skala der ursprünglichen Zeitreihe in Form von yt+1.. . yt+h rücktransformiert werden können.
Die Box-transformierte Zeitreihe (Abbildung 12 unten) weist jedoch weiterhin ein positives Trendverhalten auf. Zur Herstellung der Mittelwertstationarität kann die Differenzenoperation ∇ verwendet werden. Auch für diese existiert eine inverse Operation94, sodass eine Rücktransformation zur originären Zeitreihe stets möglich ist.
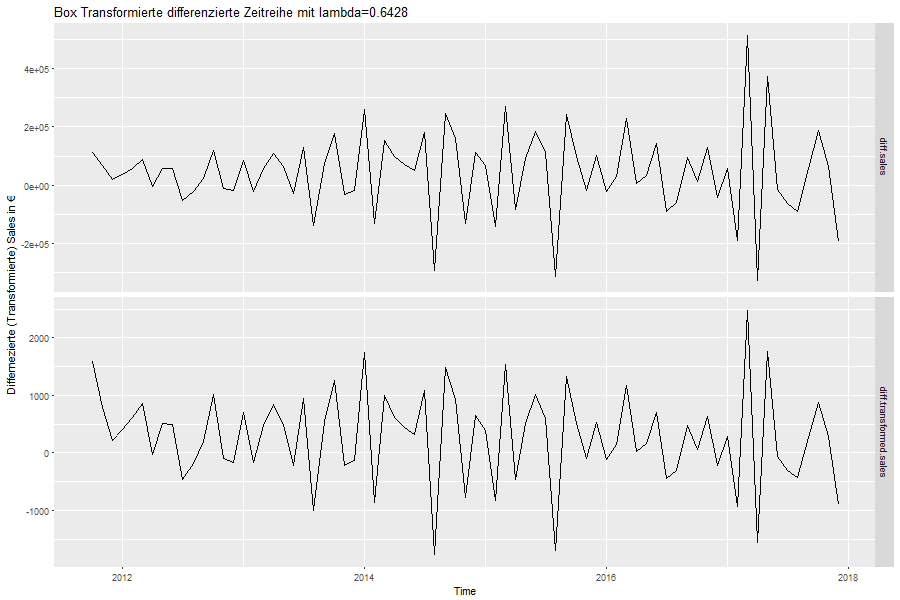
Abbildung 13 zeigt die differenzierte Zeitreihe (oben) im Vergleich zur boxtransformierten und differenzierten Zeitreihe (unten). Die Varianz der letzteren scheint durch die Transformation stabiler geworden zu sein. Eine Überprüfung der Stichprobenvarianz für verschiedene Intervalle (siehe Tabelle 3) bestätigt dies: Die Stichprobenvarianz schwankt zwischen 500 und 1100 und weist kein monotones Verhalten auf.
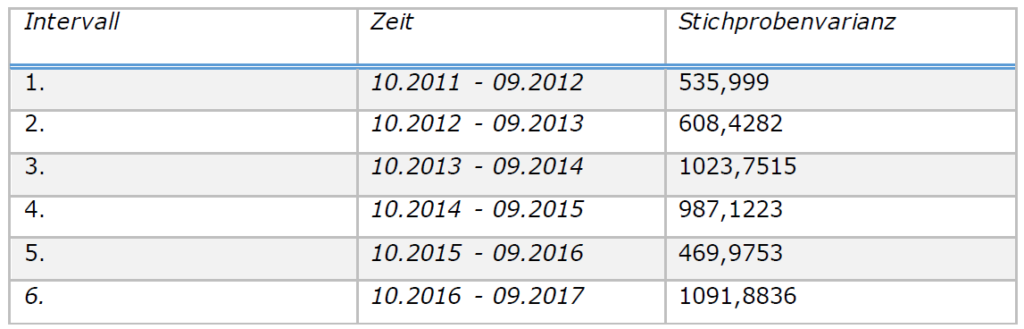
Zur Überprüfung der Stationarität wurden auch formalere Einheitswurzeltests entwickelt. Im KPSS-Test96 wird Stationarität der zu überprüfenden Zeitreihe als Nullhypothese angenommen. In Bezug auf die box-transformierte, differenzierte
Zeitreihe kann die Nullhypothese auf einem Signifikanzniveau von 10% im KPSS-Test nicht abgelehnt werden. Der formale Test bestätigt also die angenommene Stationarität.
Der nächste Schritt der Modellspezifikation besteht in Festlegung der Ordnung des ARIMA bzw. SARIMA Modells. Dazu werden die ACF (Abbildung 14 unten, links) und die PACF (Abbildung 14 unten, rechts) der box-transformierten und differenzierten Zeitreihe als unterstützendes Medium herangezogen. Festzustellen ist, dass das Verhalten beider Funktionen von den theoretisch hergeleiteten Eigenschaften für reine AR(p) bzw. MA(q) Prozesse (siehe Tabelle 1) deutlich abweicht. Die ACF weist für die Timelags τ = 1,6,7,10,12,13,18,19,20,24,25 signifikante Werte auf. Bei der PACF sind hingegen die Timelags τ = 1,2,6,10,11,12,13 signifikant. Die betrachtete Zeitreihe scheint demzufolge keinen reinen AR(p) bzw. MA(q) Prozessen zu folgen. Da die ACF nach dem Timelag τ = 1 und die PACF nach dem Timelag τ = 2 „abricht“ wird zunächst das gemischt e ARMA(1,2) Modell angenommen. Die Überlagerung des AR(2)- und MA(1)-Prozesses kann als Begründung für viele (schwach) signifikanten Timelags (τ > 2) betrachtet werden. Auffällig ist die starke Signifikanz der ACF und PACF zum Timelag τ = 12. Diese indiziert eine Erweiterung des Modells zu einem multiplikativen SARIMA Modell mit dem zusätzlichen Parameter P = 1. Berücksichtigt man die vorherige Differenzoperation ∇ als Modellparameter d = 1, so resultiert die Annahme eines multiplikat ives SARIMA(1,1,2)x(1,0,0)12 als zugrundeliegendes Modell der box-transformierte Zeitreihe. Abbildung 14:
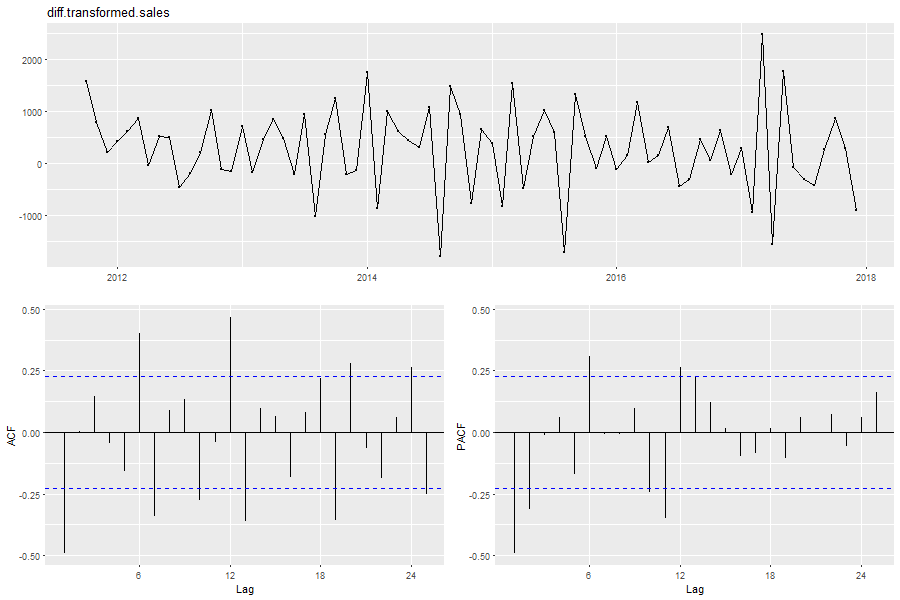
Durch die explizite Spezifikation der Modellordnung können die Parameter des Modells mit dem Maximum Likelihood Prinzip geschätzt werden. Dieses Prinzip besagt, dass unter den gegebenen Daten die wahrscheinlichsten Parameterspezifikationen gewählt werden. Formal bedeutet dies, einen Parametervektor θ aus dem p-dimensionalen Parameterraum Θ zu wählen, sodass die Likelihoodfunktion L maximiert wird:
(4.4.2) L(θ̂ |D) = 𝑠𝑢𝑝θ∈Θ L(θ|D)
Da L stets positive Werte aufweist, ist es wegen der Monotonie Eigenschaft des natürlichen Logarithmus äquivalent, das Supremum der Log-Likelihood Funktion zu ermitteln.
(4.4.3) ln L(θ̂ |D) = 𝑠𝑢𝑝θ∈Θ ln L(θ|D)
Diese Transformation erleichtert die Berechnung von θ̂ und führt dazu, dass die Werte des Einheitsintervalls [0; 1] in den gesamten Raum der negativen reellen Zahlen abgebildet werden. In Abbildung 15 ist das Ergebnis der ML-Schätzung100 der Parameter für die oben spezifizierte Modellordnung SARIMA(1,1,2)x(1,0,0)12 dargestellt.
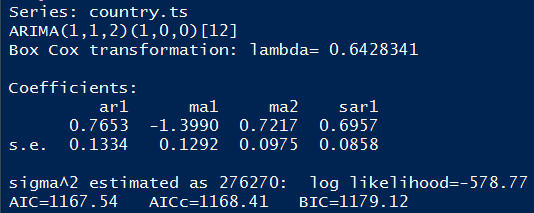
Allgemein lässt sich das Modell wie folgt formulieren:
(4.4.4) (1 − ϕ1𝐵)(1 − Φ1𝐵12)(1 − B)yt = ϵ𝑡 + θ1 ϵ𝑡−1 + θ1 ϵ𝑡−2
Mit ∇𝑦𝑡 = (1 − B)𝑦𝑡 = 𝑦𝑡 ′ und Umstellung der Gleichung ergibt sich:
(4.4.5) 𝑦𝑡 ′ = ϕ1𝑦𝑡 −1 ′ + Φ1𝑦𝑡−12 ′ + ϵ𝑡 + θ1 ϵ𝑡−1 + θ1 ϵ𝑡−2
Setzt man die geschätzten Parameter aus Abbildung 15 ein so erhält man:
(4.4.6) 𝑦𝑡 ′ = −0,7653 𝑦𝑡−1 ′ + 0,6957 𝑦𝑡−12 ′ + −1,3990 𝜖𝑡−1 + 0,7217𝜖𝑡−2 + 𝜖𝑡 𝑚𝑖𝑡 σϵ 2 = 276270
Der Wert der Log-Likelihood Funktion beträgt -578,77. Dieser Wert wird verwendet, um Informationskriterien zu kalkulieren, die in Abbildung 15 ebenfalls aufgeführt sind. Diese unterstützen dabei, innerhalb einer Modellklasse (z.B. ARIMA Modelle) die beste Modellordnung zu ermitteln. Die Informationskriterien beruhen auf dem Prinzip der Sparsamkeit101. Dieses besagt, dass unter potenziell geeigneten Modellen, diejenigen bevorzugt werden, die die geringste Anzahl an zu schätzenden Parametern aufweisen. Die Idee dahinter besteht darin, dass eine höhere Anzahl von Parametern tendenziell die „Anpassung“ des Modells an die beobachteten Daten erhöht. Ziel eines Prognosemodells ist jedoch nicht die optimale Anpassung des Modells an historische Daten, sondern die Identifikation von Zusammenhängen und Strukturen, von denen angenommen wird, dass sie über den Beobachtungshorizont hinaus existieren. Es sollten demnach nur Parameter ins Modell integriert werden, die die Erklärungskraft des Modells merklich erhöhen. In diesem Zusammenhang ist das Akaike Informationskriterium (AIC) zu betrachteten. Dieses ist definiert als:
(4.4.7) AIC = −2 ln 𝐿 + 2 p
Die Güte der Modellanpassung wird über die Log-Likelihood Funktion ausgedrückt. Eine schlechtere Modellanpassung führt zu kleinen Wahrscheinlichkeiten (Likelihood), die über den natürlichen Logarithmus auf negative Werte abgebildet werden. Durch den Koeffizienten -2 werden die Werte wiederum auf einen positiven Bereich der reellen Zahlen abgebildet. Nach diesen Transformationen (−2 ln L) stehen kleinere Werte demnach für eine bessere Modellanpassung als größere Werte. Insgesamt sollte demnach das Modell mit dem kleinsten AIC gewählt werden. Die Komponente 2p des AIC kann demnach als Strafterm für die benötigte Anzahl an Parametern p betrachtet werden. Neben dem AIC werden in Abbildung 15 auch das korrigierte AIC (AICc) sowie das Bayessche Informationskriterium (BIC) aufgelistet. Diese sind mit n als Anzahl der Beobachtungen wie folgt definiert:
(4.4.8) AICc = AIC + 2 p (p+1) 𝑛 − 𝑝−1
(4.4.9) BIC = − 2 ln 𝐿 + p ln n
Aus (4.4.8) ist ersichtlich, dass das korrigierte AICc die Anzahl der Parameter im Vergleich zum AIC mit einem weiteren Strafterm bestraft. Es wird insbesondere für Zeitreihen mit wenig Beobachtungswerten empfohlen, da das AIC und auch das BIC nur asymptotische Gültigkeit aufweisen.104 Vergleicht man die Strafterme des BIC und des AIC so ist ersichtlich, dass das BIC für n > e2 eine höhere Anzahl an Parametern stärker sanktioniert. In den meisten Fällen geben AIC, AICc sowie BIC die gleiche Empfehlung für die Auswahl einer Modellordnung. Weil für die empirischen Zeitreihen des Fallbeispiels stets weniger als 100 Beobachtungen vorliegen, werden im Rahmen dieser Arbeit die Modellparametrisierungen mit dem kleinsten AICc gewählt. In Zusammenhang mit ARIMA Modellen ist es wichtig anzumerken, dass die Informationskriterien lediglich geeignet sind, um p und q „richtig“ zu parametrisiere n. Die Anzahl der Differenzoperationen d muss zuvor festgelegt werden. Dies ist darin begründet, dass sich durch die Differenzoperation die Daten selbst verändern und die differenzierte Zeitreihe eine Beobachtung weniger aufweist. Weil die Informationskriterien über die Log-Likelihood Schätzung von den Daten selbst abhängen, sind ARIMA Modelle mit unterschiedlichem Parameter d nicht über diese Kriterien zu vergleichen.
Die Modellparametrisierung SARIMA(1,1,2)x(1,0,0)12 wurde auf Basis des Verhaltens der ACF und PACF gewählt. Diese sind gute Mittel, um die Charakteristika der Zeitreihe zu verstehen. In Bezug auf die Wahl einer geeigneten Modellparametrisierung stellen sie eine Heuristik dar. Es ist in jedem Fall sinnvoll, verschiedene (abgewandelte) Modellparametrisierungen zu berechnen und die nach den Informationskriterien beste Parametrisierung auszuwählen. Für das Beispiel Spanien zeigt sich, dass das das Ersetzen der AR(p) Komponente durch eine Konstante (Drift)106 zu einem besseren Modell nach den drei Informationskriterien führt. AIC, AICc und BIC des SARIMA(0,1,2)x(1,0,0)12 Modells aus Abbildung 16 sind jeweils niedriger im Vergleich zum vorherigen Modell (siehe Abbildung 15).
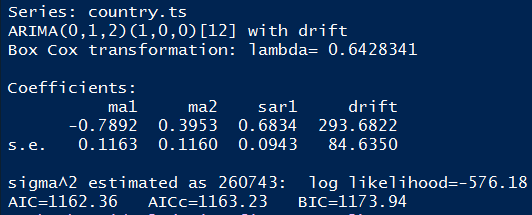
Abschließend ist eine Überprüfung der Residuen (et = 𝑦𝑡 − 𝑦𝑡 ̂ ) des Modells erforderlich.Diese sollten gemäß den Modellannahmen folgende Eigenschaften aufweisen:
1. Der Durchschnitt über alle Residuen sollte ca. 0 betragen.
2. Die Residuen sollten keine Autokorrelation mehr aufweisen.
Folgende zwei Eigenschaften sind nicht obligatorisch für ein gutes Modell, vereinfachen aber die Berechnung von Konfidenzintervallen der Forecasts:
3. Die Varianz der Residuen ist konstant.
4. Die Residuen folgen einer Normalverteilung.
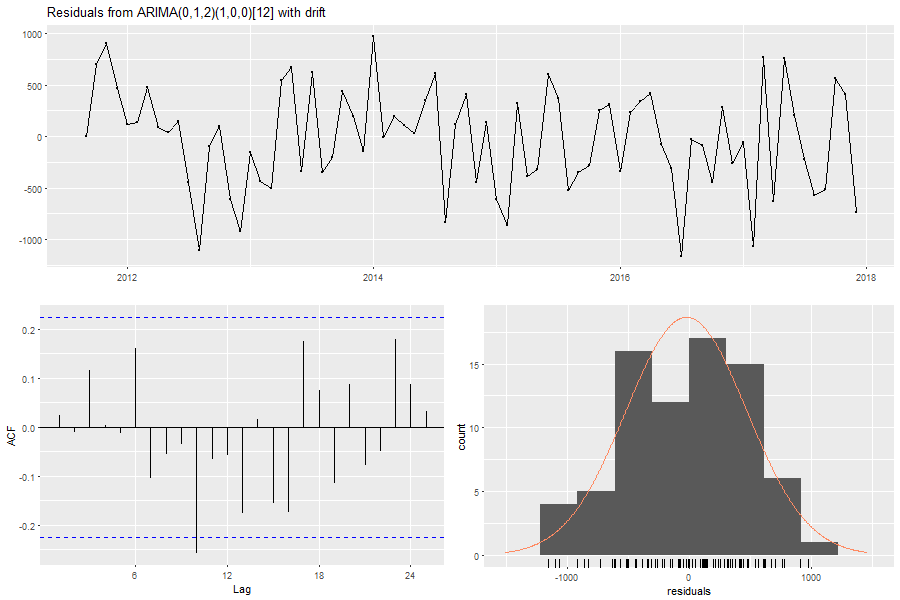
Die Zeitreihe der Residuen scheint um das Nullniveau in unvorhersehbarer Weise zu oszillieren (siehe Abbildung 17 oben). Der Durchschnitt der Residuen 𝑒𝑡 beträgt -25,60. Die erste Eigenschaft kann demnach als erfüllt angesehen werden. Das Korrelogramm der Residuen (siehe Abbildung 17 unten links) zeigt ein signifikantes Timelag für τ = 10 an. Dies ist jedoch nicht ausreichend, um die zweite Eigenschaft der Unkorreliertheit für das gewählte SARIMA Modell abzulehnen, da die Signifikanz des Timelags auch durch Zufall entstanden sein könnte.
Zur Überprüfung der Unkorreliertheit existieren deshalb formale „Portmanteau-Tests“.Diese nehmen als Nullhypothese an, dass die Autokorrelationskoeffizienten zu den ersten h Timelags jeweils null betragen. Die in Gleichung (4.4.10) gegebene Teststatistik
des Ljung-Box Tests folgt unter Annahme der Nullhypothese näherungsweise der χ2- Verteilung mit h Freiheitsgeraden.
(4.4.10) QLB = 𝑛(𝑛 + 2) Σ ρj ̂ ℎ 𝑗 =1 (j) 1 (𝑛−𝑗)
Für die Residuen des SARIMA(2,1,0)x(1,0,0)12 kann die Nullhypothese für die ersten 24 Timelags auf einem Signifikanzniveau von α = 0.05 nicht abgelehnt werden.
Die obligatorischen ersten beiden Eigenschaften der Residuen scheinen somit erfüllt zu sein. Die Annahme einer konstanten Varianz kann ebenfalls als erfüllt angesehen werden, da die Zeitreihe der Residuen in unterschiedlichen Abschnitten ähnlich111 starke Fluktuationen aufweist. Das Histogramm der Residuen in Abbildung 17 zeigt jedoch eher eine bimodale Verteilung. Die vierte Eigenschaft ist demnach nic ht gegeben. Insgesamt führt die Diagnose der Residuen dazu, dass SARIMA(0,1,2)x(1,0,0)12 Modell (mit Drift) als finales Modell zur Erklärung der spanischen Zeitreihe auszuwählen.
Die am Beispiel Spanien präsentierten Schritte der Modellspezifikation
1. Herstellung der Varianzstationarität über Box-Transformation (optional)
2. Herstellung der Mittelwertstationarität über Differenz Operation
3. Schätzung potentieller Modellparametrisierung anhand von ACF und PACF
4. Schätzung der Modellparameter mit ML-Schätzung
5. Selektion der besten Modellparametrisierung anhand des AICc Kriteriums
6. Diagnose der Residuen
wurden für die 13 Länder durchgeführt. Im Anhang 2 sind die Modellspezifikationen aller Länder dargestellt. Im Folgenden werden wesentliche Punkte ausgeführt, die bei der Modellformulierung auffällig erschienen:
1.) In den Ländern Österreich, Deutschland, Schweiz sowie dem Vereinigten Königreich konnte trotz Box-Transformation und Differenzoperation keine ideale Varianzstationarität hergestellt werden. Charakteristisch war, dass die empirische Stichprobenvarianz in den ersten 4-5 Jahresintervallen nach der Einführung monoton anstieg und für die Folgejahre abflachte und stabiler wurde. Die getroffene Annahme der Stationarität ist daher für diese Länder kritisch zu betrachten.
2.) Für die Niederlande (38 Beobachtungen) und Belgien (27 Beobachtungen) standen relativ kurze Zeitreihen zur Verfügung. In der Literatur wird der Einsatz von ARIMA Modellen für Zeitreihen mit mindestens 50 Datenpunkten empfohlen.112
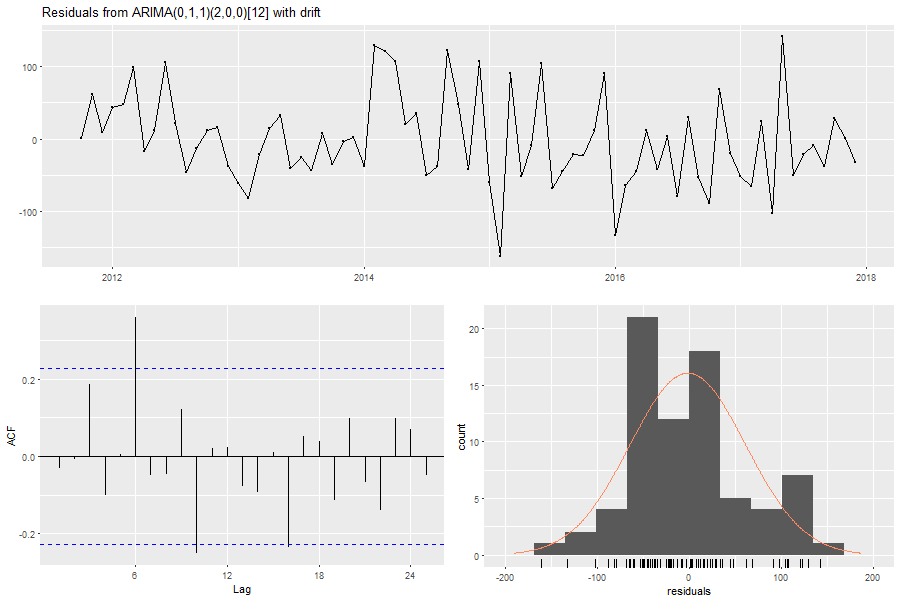
3.) In den Ländern Dänemark, Norwegen, Spanien, Schweiz sowie dem Vereinigten Königreich war die ACF zum Timelag τ = 6 im deutlich signifikantem Bereich. In Bezug auf die Schweiz wäre nach einer Box-Transformation mit λ = 0,6428 das SARIMA(0,1,1)x(1,0,0)12 nach dem Informationskriterium AICc zu wählen. Allerdings sind bei diesem Modell die Residuen zum Timlag τ = 6 signifikant miteinander korreliert (siehe Abbildung 18). Weil in der Folge auch der Ljung- Box Test für dieses Modell scheitert (die Nullhypothese der nichtkorreliert en Timelags ablehnt), wurde stattdessen ein SARIMA(0,1,6)x(1,0,0)12 Modell gewählt, welches diesem Sachverhalt Rechnung trägt. Der Preis, um Autokorrelation in den Residuen zu umgehen, ist somit ein weniger sparsames Modell, welches sich gut an die historischen Daten anpasst (kleinere Likelihood), aber unnötig113 viele Parameter enthält.
4.) In allen Ländern außer Österreich und Belgien werden saisonale Beziehungen ins Modell integriert (d.h. Verwendung von SARIMA-Modellen).
5.) Es ist länderübergreifend keine einheitliche Parametrisierung zu erkennen. Dies ist zum Teil darin begründet, dass unterschiedliche Box-Transformationen auf die originären Zeitreihen angewendet wurden und die weitere Modellschätzung auf den transformierten Zeitreihen operiert.

Recent Comments