ARIMA Modelle stellen eine Methodik der univariaten Zeitreihenanalyse dar, die auf Box und Jenkins zurückgeht. Neben den Modellen der exponentiellen Glättung zählen sie zu den gängigsten Ansätzen im Forecasting von Zeitreihen.
Innerhalb dieses Ansatzes werden Zeitreihen als Realisationen von stochastischen Prozessen definiert:
Definition 3.2.1: Stochastischer Prozess, Zeitreihe
Ein stochastischer Prozess ist eine Folge {𝑋𝑡 , t ∈ T} von Zufallsvariablen. Der Index t ∈ T wird i.d.R. als Zeit aufgefasst, wobei T=ℕ oder T=ℝ gilt. Eine Zeitreihe ist eine Folge 𝑥1, …, 𝑥𝑁 von Realisationen eines Ausschnittes von 𝑋𝑡 .
Anders gewendet kann man den stochastischen Prozess als erzeugenden Mechanismus der Zeitreihe begreifen. Definition 3.2.1 zeigt, dass ein wesentlicher Unterschied zur klassischen Statistik darin besteht, dass empirisch betrachtet nur eine Beobachtungssequenz vorliegt. Das bedeutet, dass für die verschiedenen Zufallsvariablen Xt an den jeweiligen Zeitpunkten lediglich eine Beobachtung zur Verfügung steht. Um aus den Daten dennoch statistisch gültige Schlüsse zu ziehen, wird die zentrale Forderung der Stationarität aufgestellt. Stationarität gewährleistet, dass die „stochastischen Charakteristika“32 zeitlich konstant bleiben. Dies lässt sich formal definieren:
Definition 3.2.2: Stationarität
Ein stochastischer Prozess { 𝑋𝑡 , t ∈ T} heißt (schwach) stationär, wenn unter Voraussetzung der Existenz aller Momente zweiter Ordnung gilt:
(1.) 𝐸(𝑋𝑡 ) = 𝜇𝑥
(2.) 𝑉𝑎𝑟(𝑋𝑡 ) = 𝜎𝑥 2 > 0
(3.) 𝐶𝑜𝑣(𝑋𝑡 , 𝑋𝑠 ) = 𝛾𝑥(𝑑) 𝑚𝑖𝑡 d = t-s
für alle t ∈ T und alle d ≠ 0 (d ∈ T), wobei 𝜇𝑥, 𝜎𝑥 von t unabhängige Konstanten seien, und 𝛾𝑥(𝑑) eine von t unabhängige Funktion ist.
Die ersten beiden Bedingungen sichern, dass alle Zufallsvariablen Xt unabhängig vom Zeitpunkt den gleichen Erwartungswert bzw. die gleiche Varianz aufweisen. Die dritte Bedingung gewährleistet, dass die Kovarianz zwischen zwei Zufallsvariablen des stochastischen Prozesses allein vom zeitlichen Abstand d der Zufallsvariablen abhängig ist. Da die Zufallsvariablen aus demselben stochastischen Prozess generiert werden, bezeichnet man die Kovarianz in diesem Zusammenhang als Autokovarianz und definiert:
Definition 3.2.3: Theoretische Autokovarianz und –korrelation
Sei {𝑋𝑡 , t ∈ T} ein stochastischer Prozess, für den alle Momente der zweiten Ordnung 𝐸(𝑋𝑡 𝑋𝑠 ) existieren. Dann heißt die Funktion
(1.) 𝛾𝑥(𝑡, 𝑠) = 𝐶𝑜𝑣(𝑋𝑡 , 𝑋𝑠 ) Autokovarianzfunktion und
(2.) 𝜌𝑋 (𝑡, 𝑠) = 𝐶𝑜𝑣(𝑋𝑡,𝑋𝑠) √𝑉𝑎𝑟(𝑋𝑡)⋅𝑉𝑎𝑟(𝑋𝑠) Autokorrelationsfunktion, wobei Var(Xt) > 0
Definition 3.2.4: Empirische Autokovarianz und –korrelation
Die empirische Autokovarianzfunktion 𝑐𝜏 einer Zeitreihe 𝑦𝑡 , sowie die empirische Autokorrelationsfunktion 𝑟𝜏 (kurz ACF) sind definiert durch:
(1.) 𝑐𝜏 = 1 𝑁 Σ (𝑦𝑡 +𝜏 − 𝑦̅)(𝑦𝑡 𝑁−𝜏 − 𝑦̅) 𝑡 =1 , (𝜏 ≥ 0)
(2.) 𝑟𝜏 = 𝑐𝜏 𝑐0
Für τ > 0 wird cτ = c-τ und rτ = r-τ gesetzt.
Zur Identifikation von Abhängigkeitsstrukturen einer Zeitreihe verwendet man die grafische Repräsentation der empirischen ACF, die als Korrelogramm bezeichnet wird.
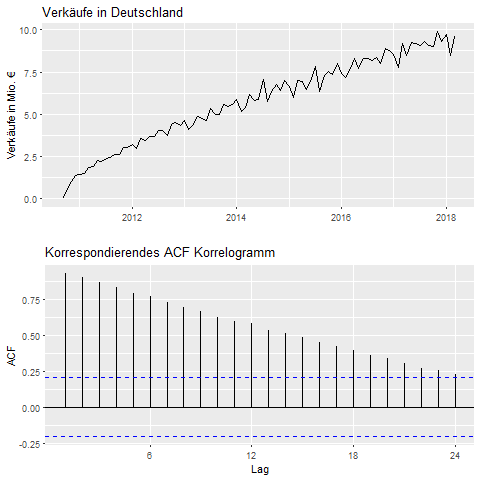
Abbildung 1 zeigt die Zeitreihe der Verkaufszahlen des Produktes Palexia der Grünenthal GmbH in Deutschland im direkten Vergleich zum korrespondierenden Korrelogramm. Der konstante Aufwärtstrend der Zeitreihe bewirkt, dass die ACF im Korrelogramm für kleine Timelags am höchsten37 ist und mit wachsendem Timelag monoton abnimmt. Interessant ist an dem Verlauf, dass die Autokorrelation für das „Timelag“ von 12 Monaten sich nicht wesentlich aus dem sonstigen Kurvenverlauf hervorhebt. Dies lässt die Interpretation zu, dass der Trend der Zeitreihe schwerer wiegt, als eine möglic he Saisonkomponente.
Neben der ACF wird auch die partielle Autokorrelationsfunktion (PACF) zur Untersuchung der Zeitreihenstruktur herangezogen. Die Idee dahinter besteht darin, nur die direkte Korrelation zwischen zwei Zufallsvariablen Xs und Xs +h mit dem Abstand (Timelag) h zu messen. Angenommen es gelte h = 2 und es bestehe eine Korrelation zwischen Xs und Xs +h unter der Prämisse der Stationarität des zugrundeliegenden stochastischen Prozesses. Zwischen den beiden Zufallsvariablen Xs und Xs+h liegt dann jeweils die Zufallsvariable Xs +1. Die partielle Autokorrelation eliminiert die indirekten Anteile der ACF, die dadurch zustande kommen können, dass Xs mit Xs+1 und Xs+1 mit Xs+2 korreliert ist. Allgemein lässt sich die PACF wie folgt definieren:
Definition 3.2.5: Partielle Autokorrelationsfunktion
Die partielle Autokorrelationsfunktion (𝜋𝜏), kurz PACF, eines stationären Prozesses (𝑋𝑡) ist die Folge der partiellen Korrelationen von 𝑋𝑡 und 𝑋𝑡 −𝜏 unter Festhalten der Werte von 𝑋𝑡 −1, … , 𝑋𝑡 −𝜏+1. Für τ=0 wird 𝜋0 = 1 und für 𝜏 = 1 wird 𝜋1 = 𝜌(1)39 gesetzt.
Nachdem die elementaren Begriffe stochastischer Prozess und Stationarität definitorisc h vorgestellt wurden, kann nun die Bedeutung des Akronyms ARIMA entschlüsselt sowie der Aufbau der ARIMA Modelle erläutert werden.
Autoregressive (AR) Modelle:
In Modellen der multiplen linearen Regression wird die abhängige statistische Variable (Regressand)Yt durch die Linearkombination mehrerer unabhängiger Variablen (Regressoren) erklärt. Von den Störgrößen ϵt wird angenommen, dass diese unabhängig, identisch Normalverteilt 𝜖𝑡 ∼ Ν(0, σε 2) sind, falls das lineare Modell „richtig“ ist:
(3.2.1) 𝑌𝑡 = Σ (𝑋𝑡𝑖 ß𝑖 𝑖=𝐾 ) 𝑖=1 + 𝜖𝑡 , 𝑓ü𝑟 𝐾 𝑢𝑛𝑎𝑏ℎä𝑛𝑔𝑖𝑔𝑒 𝑉𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑛 𝑥 1 … 𝑥𝐾
Der Begriff „Autoregressive“ zeigt an, dass eine Regression der abhängigen Variable n gegen sich selbst (gegen zeitlich frühere Zufallsvariablen desselben stochastischen Prozesses) vollzogen wird. Ein AR Modell der Ordnung p kann in folgender Form beschrieben werden:
(3.2.2) 𝑌̃𝑡 = Σ (𝜙𝑖 𝑌̃𝑡-i) 𝑖=𝑝 𝑖=1 + 𝜖𝑡 𝑚𝑖𝑡 𝑌̃𝑡 = 𝑌𝑡 − 𝜇
Durch Umstellen erhält man folgende äquivalente Darstellung, die ebenfalls von einigen Autoren verwendet wird.
(3.2.3) Yt = c + Σ (ϕi Yt−i i=p ) i =1 + ϵt mit c = μ(1 − Σ Φi pi =1 )
Mit 𝜇 𝑏𝑧𝑤. 𝑐, 𝜙1 … 𝜙𝑝 ,𝜎𝜖 2 enthält das Modell p + 2 unbekannte Parameter, die aus den Daten geschätzt werden müssen. μ ist eine Konstante, die das Niveau des stochastischen Prozesses beschreibt. 𝜙1 … 𝜙𝑝 bezeichnen die Linearkoeffizienten, mit denen die p vorangegangenen Zufallsvariablen entsprechend gewichtet werden, um die aktuelle Zufallsvariable yt zu erklären. σϵ 2 ist die konstant angenommene Varianz der unsystematischen Störungen. Die Folge der Störungsgrößen ϵt, von denen üblicherweise eine Normalverteilung angenommen wird, stellt selbst einen stochastischen Prozess dar, der in der Literatur als „White Noise“ Prozess (weißes Rauschen) bezeichnet wird.
Kompakter lässt sich das Modell mit Hilfe des Verschiebe-Operators (Backshift) B und mit Hilfe des linearen Filters ϕ(B) = 1 − ϕ1𝐵 −.. . −ϕ𝑝 𝐵 𝑝 formulieren:
(3.2.4) Ỹ t −Ỹ t Σ (ϕiBi) pi=1 = ϵt
(3.2.5) ϕ(𝐵 )𝑌̃𝑡 = 𝜖𝑡
Die Auswahl der p Linearkoeffizienten bestimmt, ob der AR(p) Prozess stationär ist. Allgemein ist ein AR(p) Prozess stationär, falls die Wurzeln des Polynoms ϕ(B) alle außerhalb des Einheitskreises liegen.Im Falle eines AR(1) Modells ist diese Bedingung erfüllt, falls |ϕ1| < 1.
Moving Average (MA) Modelle
MA(q) Modelle basieren auf der Idee, dass zufällige Störereignisse ϵt über q Perioden auf den stochastischen Prozess einwirken. Das aktuelle Störereignis ϵt fließt unverändert in den Funktionsterm ein. Störereignisse der q zurücklegenden Perioden werden mit den Koeffizienten −Θ1 … − Θq gewichtet. Wie bei AR Modellen sind das Niveau des Prozesses μ und die Varianz des White Noise Prozesse σϵ 2 Konstanten. Insgesamt müssen q + 2 Parameter durch die verfügbaren Daten geschätzt werden.
(3.2.6) 𝑌̃𝑡 = 𝜖𝑡 − Σ (𝛩𝑖 𝜖𝑡−𝑖𝑖=𝑞 ) 𝑖=1
(3.2.6) lässt wiederum kompakter mit dem linearen Filter Θ(B) = 1 − Σi=q(ΘiBi) i=1 schreiben:
(3.2.7) 𝑌𝑡 = 𝜇 + 𝜖𝑡𝛩(𝐵)
Im Gegensatz zu AR Prozessen sind MA Prozesse stets (schwach) stationär, wie gezeigt werden kann:
E[Yt ] = E[𝜇 + 𝜖𝑡 − Θ1𝜖𝑡−1 … − Θq 𝜖𝑡−𝑞 ]
= E[𝜇] + 𝐸[ϵ𝑡 ] − Θ1𝐸[ϵ𝑡−1] − Θ𝑞𝐸[ϵ𝑡−𝑞 ]
= μ ,da E[ϵt ] = 0, für alle t (Definition des White Noise Prozesses )
VAR[Yt ] = E[(Yt )2] − (E[Yt ])2
= E[ (𝜇 + 𝜖𝑡 − Θ1𝜖𝑡−1 … − Θq 𝜖𝑡−𝑞) (𝜇 + 𝜖𝑡 − Θ1𝜖𝑡−1 … − Θq 𝜖𝑡−𝑞) ] − 𝜇2
= E[𝜇2] + Θ1 2E[(ϵt−1)2] + ⋯ + Θq 2E[(ϵt−q)2 ] − 𝜇2, 𝑤𝑒𝑖𝑙 𝐸[𝜖𝑡 𝜖𝑠] = 0 𝑓ü𝑟 𝑡 ≠ 𝑠
= σϵ 2(1 + Σ Θ𝑖 2 ) 𝑞𝑖 =1 𝑚𝑖𝑡 𝐸[(𝜖𝑡 )2] = 𝜎𝜖 2 𝑓ü𝑟 𝑎𝑙𝑙𝑒 𝑡
𝐶𝑂𝑉[𝑌𝑡 ,𝑌𝑡−𝑘] = 𝛾𝑌 (𝑡, (𝑡 − 𝑘)) = 𝐸[𝑦𝑡 𝑦𝑡 −𝑘] – E[𝑦𝑡 ]𝐸[𝑦𝑡 −𝑘] = 𝐸[𝑦𝑡 𝑦𝑡 −𝑘] − 𝜇2
= 𝐸[(𝜇 + 𝜖𝑡 − 𝛩1𝜖𝑡−1 … − 𝛩𝑞 𝜖𝑡−𝑞) (𝜇 + 𝜖𝑡 −𝑘 − 𝛩1𝜖𝑡−1−𝑘 … − 𝛩𝑞 𝜖𝑡−𝑞−𝑘)
= 𝐸[𝜇 2] − 𝛩𝑘 𝐸[(𝜖𝑡 −𝑘)2] + 𝛩𝑘+1𝛩1𝐸[(𝜖𝑡 −𝑘−1)2] + ⋯ + 𝛩𝑞𝛩𝑞 −𝑘𝐸 [(𝜖𝑡−𝑘−𝑞)2] − 𝜇2
= 𝜎𝜖 2(−𝛩𝑘 + 𝛩𝑘+1𝛩1 + ⋯ + 𝛩𝑞𝛩𝑞−𝑘 ) 𝑚𝑖𝑡 𝛩0 = −1 𝑢𝑛𝑑 𝑘 = 1 . . . 𝑞
Daraus folgt:
(3.2.8) γY (t, (𝑡 − 𝑘)) = γY (k) = {σϵ 2 (−Θk + Θk+1 Θ1 + ⋯ + Θq Θq−k ) , für k = 1. . . q 0 , für k > q
Weil Erwartungswert und Varianz lediglich von den Konstanten (𝜇 𝑏𝑧𝑤 . 𝜎𝜖 2 sowie Θ1 … Θ𝑞 ) abhängen, sind sie selbst konstant und damit zeitunabhängig. Da weiterhin die theoretische Autokovarianz ausschließlich vom Zeitabstand (Timelag) nicht aber von den Zeitpunkten der Zufallsvariablen abhängig ist, sind die drei Bedingungen der Stationarität aus Definition 3.2.2 erfüllt.
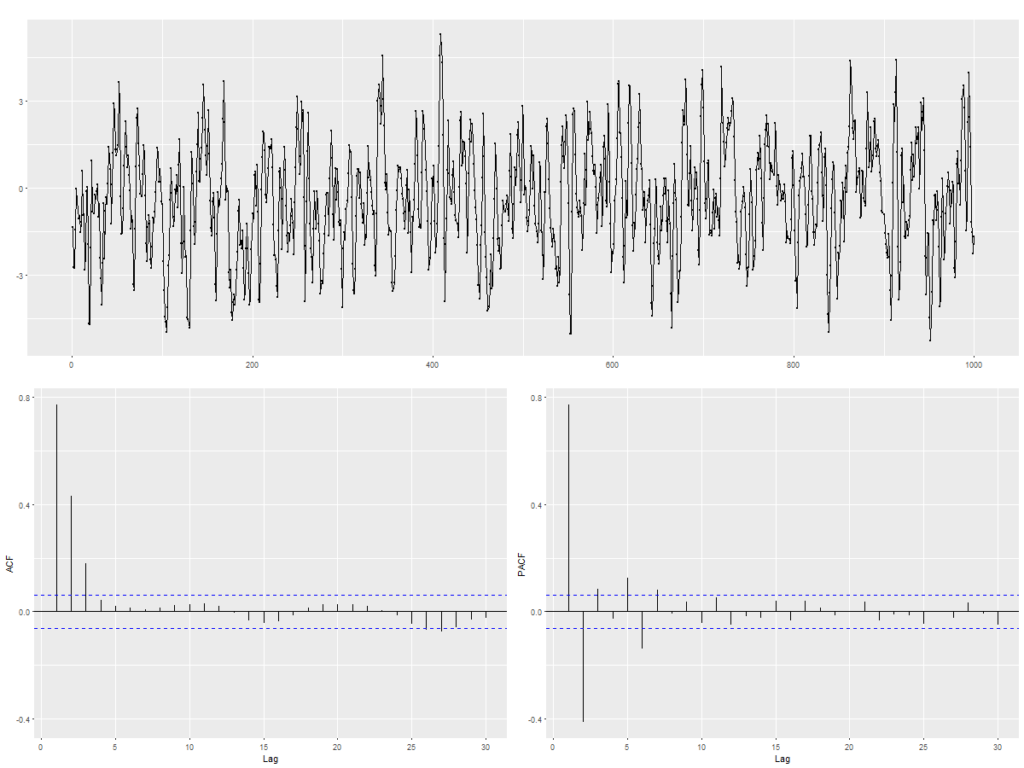
Die theoretisch hergeleitete Autokovarianz für Moving Average Prozesse aus (3.2.8) weist die Eigenschaft auf, für Timelags k > q abzubrechen, d.h. dass nach den ersten q Timelags alle Autokovarianzen den Wert 0 annehmen. Dies ist für die praktische Anwendung bedeutsam, um unter Betrachtung der empirischen ACF auf einen MA Prozess als treibenden stochastischen Mechanismus zu schließen. Abbildung 2 zeigt die Realisation (t = 1 … 1000) eines MA(3) Prozesses mit folgender Parametrisierung:
Yt = μ + ϵt + Θ1 ϵt−1 + Θ2 ϵt−2 + Θ3 ϵt−3
= 0 + ϵt + 1,2ϵt−1 + 0,8ϵt−2 + 0,4 ϵt−3 ,𝑚𝑖𝑡 σϵ 2 = 1
Im Korrelogramm (unten links) ist das Abrechen der ACF nach dem Timelag k=3 deutlich zu erkennen. Im Unterschied zur theoretischen Herleitung beträgt ist die ACF nicht exakt null, verbleibt aber innerhalb eines Bereiches (blau gestrichelte Linien), der nicht signifikant von 0 abweicht und durch empirische Zufälle in der Stichprobenziehung zu erklären ist.
Allgemein lassen sich folgende theoretische Eigenschaften der ACF und PACF herleiten, die für die Identifikation von Modellparametern von Bedeutung sind:

ARIMA Modelle
Das Akronym ARIMA kann in die drei Komponenten AR (Autoregressive), I (Integrated)
und MA (Moving Average) zerlegt werden. In einer Vorstufe werden zunächst
sogenannte ARMA(p, q) Modelle dargestellt, die aus den bereits vorgestellten AR und MA
Modellen komponiert werden:
(3.2.9) 𝑌̃𝑡 = Σ (𝛷𝑖 𝑌̃𝑡−𝑖) 𝑝𝑖 =1 + 𝜖𝑡 + Σ (−𝛩𝑖𝑞𝑗=1 𝜖𝑡 −𝑗)
Das ARMA Modell enthält folglich p + q + 2 Parameter, die geschätzt werden müssen.
Durch Verwendung der bereits eingeführten linearen Filter Θ(𝐵) und Φ(𝐵) ergibt sich die
kompaktere Darstellung:
(3.2.10) Φ(B)Ỹt = Θ(𝐵)ϵ𝑡
AR, MA sowie ARMA Modelle setzen die Stationarität Ihrer stochastischen Prozesse
voraus. Viele empirische Zeitreihen weisen jedoch nichtstationäres Verhalten auf, da sie
z.B. durch Trends und saisonale Schwankungen gekennzeichnet sind. Oftmals sind sie
aber dennoch über ein homogenes zeitliches Verhalten gekennzeichnet. Um die
eingeführte Methodik auch auf diese Klasse von Zeitreihen anwenden zu können, wird
das ARMA(p, q) Modell um den Parameter d zum ARIMA (p, d, q) Modell erweitert. Dieser
Parameter gibt an, wie häufig die Differenzoperation ∇ = (1 − B) angewendet werden
muss, um die Annahme von Stationarität treffen zu können. Dies soll an folgendem
Beispiel verdeutlicht werden:
Gegeben sei das folgende ARMA(1,1) Modell:
(3.2.11) 𝑌𝑡 = 𝑌𝑡−1 + 𝜖𝑡 − Θ1𝜖𝑡−1,mit |Θ1| < 1
Mit einem Widerspruchsbeweis lässt sich formal zeigen, dass keine schwach stationäre
Lösung 𝑌𝑡 existiert.
Durch geeignete Transformation kann der Lösungsprozess Yt stationarisiert werden:
Sei 𝑊𝑡 = ∇𝑌𝑡 = 𝑌𝑡 − 𝑌𝑡−1, dann erhält man aus (3.2.11)
(3.2.12) 𝑊𝑡 = 𝜖𝑡 − Θ1𝜖𝑡−1, 𝑚𝑖𝑡 |Θ1| < 1
Der in (3.2.12) formulierte Prozess 𝑊𝑡 ist ein endlicher MA-Prozess und somit schwach
stationär.
Ein Arima Modell kann folglich allgemein mit folgender Gleichung formuliert werden:
(3.2.13) Φ(𝐵)ω𝑡 = Θ(𝐵)𝜖𝑡 ,𝑤𝑜𝑏𝑒𝑖 ω𝑡 = (1 − 𝐵)𝑑 𝑌𝑡
Unter Verwendung des Differenzenoperators ∇ erhält man die finale Darstellung:
(3.2.14) Φ(𝐵) ∇𝑑 𝑌𝑡 = Θ(𝐵)𝜖𝑡
Saisonale Arima Modelle
ARIMA(p, d, q) Modelle können um weitere Terme ergänzt werden, die Abhängigkeiten
von Zeitreihenwerten berücksichtigen, die sich um ein Vielfaches der Periodenlänge s
unterschieden.
Zunächst wird ein einfaches saisonales ARIMA Modell SARIMA (P, D, Q)s betrachtet,
welches wie das klassische ARIMA Modell aufgebaut ist. Die Operationen ∇ und die
linearen Filter Φ(B) und Θ(B) werden so angepasst, dass sie jeweils auf Werten der
Vorperiode operieren:
∇s= 1 − Bs
Φ𝑠(𝐵 𝑠) = 1 − Φ1𝐵 𝑠 − Φ2 𝐵 2𝑠 −. .. −Φ𝑃 𝐵 𝑃𝑠
Θs(Bs) = 1 − Θ1Bs − Θ2B2𝑠 −. . . −ΘQ B𝑄𝑠
Mit diesen Operatoren und der ARIMA Modellgleichung Φ(𝐵) ∇𝑑 𝑌𝑡 = Θ(𝐵)𝜖𝑡 erhält man:
(3.2.15) Φ𝑠(𝐵 𝑠) ∇s
𝐷 𝑌𝑡 = Θs(Bs)u𝑡 , 𝑤𝑜𝑏𝑒𝑖 𝑢𝑡 𝑒𝑖𝑛𝑒𝑚 𝑊ℎ𝑖𝑡𝑒 𝑁𝑜𝑖𝑠𝑒 𝑃𝑟𝑜𝑧𝑒𝑠𝑠 𝑒𝑛𝑡𝑠𝑝𝑟𝑖𝑐ℎ𝑡
Setzt man für ut statt einem White Noise Prozess wiederum das klassische ARIMA Modell
an, so lassen sich Abhängigkeiten zwischen direkt aufeinanderfolgenden Werten in das
Modell integrieren.54 ut erfüllt dann:
(3.2.16) Φ(𝐵) ∇𝑑 𝑢𝑡 = Θ(𝐵)𝜖𝑡
(3.2.17) 𝑢𝑡 = Θ(𝐵)(Φ(𝐵))−1( ∇𝑑 )−1ϵt
Eingesetzt in (3.2.15) und mit formalen Umstellen ergibt sich die Modellgleichung eines
multiplikativen SARIMA(p, d, q)x(P, D,Q)s Modells:
(3.2.18) ϕ(𝐵) Φ𝑠 (𝐵 𝑠) ∇𝑑 ∇s𝐷 𝑌𝑡 = Θ(𝐵) Θs(Bs)ϵt
Aufgrund der Generalität bilden alle zuvor vorgestellten Modelle Spezialfälle des multiplikativen SARIMA Modells, die durch geeignete Parametrisierung erzeugt warden können.

Recent Comments