Eine weitere bedeutsame Klasse von Prognosemodellen stellen sogenannte ETS Modelle dar, die in der Fachsprache auch unter dem englischen Begriff „State Space Models“ diskutiert werden56. Das Akronym ETS kann als Stellvertreter für zwei unterschiedliche Termini stehen. Zunächst kann es als Abkürzung für die Wortgruppe „ExponenTial Smoothing“ (Exponentielle Glättung) gedeutet werden. Auf die Methoden der exponentiellen Glättung wird zunächst eingegangen, da sie den konzeptionellen Ursprung der ETS Modelle bilden. Die Methoden blicken auf eine lange Historie zurück und wurden insbesondere von Brown, Holt und Winters entwickelt.
In Abschnitt 3.1 wurde die begriffliche Unterscheidung zwischen Prediction und Forecast getroffen. Diese wird an dieser Stelle relevant, da die herkömmlichen Methoden der exponentiellen Glättung lediglich für Punktschätzungen (Predictions) geeignet waren.58 Anhand der originären „Simple Exponential Smoothing Method“ von Brown kann die Kernidee der klassischen Methoden verdeutlicht werden:
Angenommen es seien observierte Daten bis einschließlich Zeitpunkt t − 1 verfügbar. 𝑦̂𝑡 bezeichne die Punktschätzung der Zielvariable in Periode t. Wird die Beobachtung 𝑦𝑡 verfügbar, ergibt sich der Fehler der Vorhersage aus 𝑦𝑡 − 𝑦̂𝑡 . Für die Folgeperiode kann der folgende Forecast formuliert werden:
(3.3.1) 𝑦̂𝑡+1| 𝑡 = 𝑦̂𝑡 + α (𝑦𝑡 − 𝑦̂ )
Die neue Schätzung 𝑦̂𝑡+1| 𝑡 ergibt sich folglich aus der alten Schätzung 𝑦̂ , die um den mit α gewichteten Prognosefehler korrigiert wird. Der Parameter α ∈ [0; 1] determiniert wie stark neue Schätzungen um aufgetretene Prognosefehler korrigiert werden. Gleichung (3.3.1) kann in folgende Form umgestellt werden, die verdeutlicht, dass die neue Schätzung gleichsam einen gewichteten Durchschnitt zwischen neuer Beobachtung 𝑦𝑡 und alter Schätzung 𝑦̂ , darstellt.
(3.3.2) 𝑦̂𝑡+1| 𝑡 = α 𝑦𝑡 + (1 − α) 𝑦̂𝑡
Durch rekursives Einsetzen von Gleichung (3.3.2) in 𝑦̂𝑡 bis hin zu 𝑦̂1 erhält man:
(3.3.3) 𝑦̂𝑡+1| 𝑡 = α𝑦𝑡 + α(1 − α)𝑦𝑡 −1 + α(1 − α)2𝑦𝑡 −2 + ⋯ + α(1 − α)t−1𝑦1 + (1 − α)𝑡 𝑦̂1
𝑦̂𝑡+1| 𝑡 repräsentiert folglich einen gleitenden Durchschnitt aller vergangenen Beobachtungen, die mit exponentiell60 abnehmenden Koeffizienten gewichtet werden. Die Schätzung für den ersten Zeitpunkt 𝑦̂1 fließt mit (1 − α) in die Schätzung ein und hat ein höheres Gewicht, sofern der Parameter α klein gewählt wird. Um Prognosen für 𝑦̂𝑡+1| 𝑡 zu erstellen, müssen folglich α und 𝑦̂1 geschätzt werden.
Eine alternative Repräsentation von Gleichung (3.3.3) (Gewichteter Durchschnitt) ist die sogenannte Komponenten Form. In dieser Schreibweise lässt sich (3.3.3) wie folgt formulieren:
(3.3.4.a) 𝐿𝑒𝑣𝑒𝑙: lt = α 𝑦𝑡 + (1 − α)lt−1
(3.3.4.b) Prognose: 𝑦̂𝑡 +ℎ = lt (3.3.4.b) stellt die Prognosegleichung da, wohingegen Gleichung (3.3.4.a) die Transformationsgleichung des Levels l beschreibt. Das initiale Level l0 dieser Darstellung entspricht folglich 𝑦̂1 aus Gleichung (3.3.3)
Die Komponenten Form wirkt zunächst „umständlich“, hat aber den Vorteil, dass sich Browns „Simple Exponential Method“ in dieser Form verständlich erweitern lässt:
(3.3.5.a) 𝐿𝑒𝑣𝑒𝑙: 𝑙𝑡 = 𝛼 𝑦𝑡 + (1 − 𝛼) (𝑙𝑡−1 + 𝑏𝑡−1)
(3.3.5.b) 𝑇𝑟𝑒𝑛 : b𝑡 = 𝛽∗ (𝑙𝑡 − 𝑙𝑡−1) + (1 − 𝛽∗) bt−1
(3.3.5.c) 𝑃𝑟𝑜𝑔𝑛𝑜𝑠𝑒 : 𝑦̂𝑡 +ℎ = 𝑙𝑡 + 𝑏𝑡 ℎ
Diese drei Gleichungen beschreiben eine Erweiterung, die auf die Arbeit von Holt63 zurückgeht. Die originäre Methode von Brown wird durch eine lineare Trendkomponent e (3.3.5.b) erweitert, die wiederum einen gewichteten Durchschnitt aus geschätzter vorheriger Trendkomponente bt−1 und aktueller Steigung (ausgedrückt durch die Differenz aufeinander folgender Level lt − lt−1) bildet. In diesem Fall müssen demnac h die Glättungskonstanten α, β∗ sowie die initialen Schätzungen für Level l0 und Trend b0 spezifiziert werden, um Prognosen für zukünftige Perioden zu erstellen. Basierend auf der Methode von Holt wird nun der Zusammenhang zu den unterliegenden „State Space“ Modellen hergestellt.
Zunächst wird die Setzung μt = 𝑦̂𝑡 = lt−1 + bt−1 vorgenommen.64 Der Erwartungswert des neu konstruierten stochastischen Prozesses entspricht dadurch dem Punktschätzer der klassischen Methode nach Holt zu allen Zeitpunkten t. ϵt = 𝑦𝑡 − 𝑦̂𝑡 bezeichne den Fehler der Ein-Schritt Vorhersage. Für ϵt wird in der Regel eine Normalverteilung mit dem Erwartungswert 0 angenommen: ϵt ~ N(0, σ2). Mit diesen Annahmen lassen sich drei neue Gleichungen bilden, die das additive State Space Modell beschreiben:
(3.3.6.a) 𝑦𝑡 = 𝑦̂𝑡 + 𝜖𝑡 = 𝑙𝑡−1 + 𝑏𝑡−1 + 𝜖𝑡
(3.3.6.b) lt = α(lt−1 + bt−1 + ϵt ) + (1 − α)(𝑙𝑡−1 + 𝑏𝑡−1) = 𝑙𝑡−1 + 𝑏𝑡−1 + αϵt
(3.3.6.c) b𝑡 = 𝛽∗ (𝑙𝑡−1 + 𝑏𝑡−1 + αϵt − 𝑙𝑡−1) + (1 − 𝛽∗) bt−1 = bt−1 + α𝛽∗ϵt
Die Konstante αβ∗ der letzten Gleichung wird in der Literatur meist mit β bezeichnet.65 Insgesamt spezifizieren die drei Gleichungen das State Space Modell. Dieses beschreibt einen stochastischen Prozess, sodass im Gegensatz zur linearen Methode von Holt nicht nur eine Punktschätzung, sondern auch die Wahrscheinlichkeitsverteilung der Zielvariable yt für zukünftige Zeitpunkte ermittelt werden kann.
Für den Fehlerterm ϵt der Einschritt Prognose wurde oben die Setzung ϵt = 𝑦𝑡 − 𝑦̂𝑡 vorgenommen. Dadurch besitzt der (absolute) Fehlerterm die gleiche Einheit wie die Zielvariable. Da ϵt und die ursprüngliche Schätzung additiv zusammengefasst werden, bezeichnet man (3.3.6) als additives State Space Modell.
Alternativ kann auch ϵt = (𝑦𝑡 − 𝑦̂ )/𝑦̂𝑡 als relativer Fehler angesetzt werden. Dies führt zu einem multiplikativen State Space Modell. Unter Einbezug der klassischen Methode von Holt (3.3.5) lässt sich wiederum das folgende State Space Modell herleiten:
(3.3.7.a) yt = 𝑦̂(1 + ϵ𝑡 ) = (lt−1 + bt−1) (1 + ϵ𝑡 )
(3.3.7.b) lt = α [(lt−1 + bt−1) (1 + ϵ )] + (1 − 𝛼) (𝑙𝑡−1 + 𝑏𝑡 −1)
= αϵ𝑡 (𝑙𝑡−1 + 𝑏𝑡−1) + (𝑙𝑡−1 + 𝑏𝑡−1)
= (𝑙𝑡−1 + 𝑏𝑡−1)(1 + αϵ𝑡 )
(3.3.7.c) b𝑡 = 𝛽∗ [(𝑙𝑡−1 + 𝑏𝑡−1)(1 + αϵ𝑡 ) − 𝑙𝑡−1] + (1 − 𝛽∗) bt−1
= β∗[𝑏𝑡−1 + αϵ𝑡 (𝑙𝑡−1 + 𝑏𝑡−1)] + (1 − 𝛽∗) bt−1 = 𝑏𝑡−1 + 𝛼𝛽∗(𝑙𝑡−1 + 𝑏𝑡−1)𝜖𝑡
= bt−1 + β(𝑙𝑡−1 + 𝑏𝑡−1)ϵ𝑡 ,𝑚𝑖𝑡 αβ∗ = β
Da Schätzterm und Fehlerterm in Gleichung (3.3.7.a) multiplikativ verknüpft sind, bezeichnet man dieses als ein multiplikatives State Space Modell. Wie beim vorherigen additiven Modell weist es die Eigenschaft auf, dass der Erwartungswert von yt an allen Zeitpunkten dem Punktschätzer der klassischen Holt Methode entspricht. Es 65 Hyndman unterscheidet sich jedoch vom additiven Modell in sonstigen Eigenschaften der Wahrscheinlichkeitsverteilung des stochastischen Prozesses yt. Zum Beispiel sind die jeweiligen Konfidenzintervalle des additiven und multiplikativen Modells unterschiedlich.66 Es ist anzumerken, dass die angesprochene Gleichheit der Punktschätzer nur dann gegeben ist, falls bei Anpassung der additiven und multiplikativen Modelle jeweils die gleichen Modellparameter geschätzt werden.
Die Gleichungen (3.3.6) und (3.3.7) lassen sich eine effizientere Notation bringen, wenn man die Glättungskonstanten in dem Zustandsvektor („State Vector“) 𝒙𝒕 = (𝑙 ,𝑡 ) ′ zusammenfasst. Das multiplikative Modell aus (3.3.6) lässt sich dann in der standardisierten „State Space“ Notation schreiben:
(3.3.8.a) y_t = [1 1] 𝑥𝑡−1 (1 + ϵt ),
(3.4.8.b) 𝑥𝑡 = [1 0 11 ] 𝑥𝑡−1 + [1 1]𝑥𝑡−1 [ 𝛼 𝛽] ϵ𝑡
Nachdem der Übergang von den klassischen Methoden zu den unterliegenden State Space Modellen illustriert wurde, wird im Folgenden eine Erweiterung der linearen Methode von Holt vorgestellt, die eine saisonale Komponente in den beobachteten Zeitreihen berücksichtigt:
(3.3.9.a) 𝐿𝑒𝑣𝑒𝑙: 𝑙𝑡 = (𝑦𝑡 − 𝑠𝑡−𝑚) + (1 − 𝛼)(𝑙𝑡−1 + 𝑏𝑡−1)
(3.3.9.b) 𝑇𝑟𝑒𝑛 : b𝑡 = 𝛽∗ (𝑙𝑡 − 𝑙𝑡−1) + (1 − 𝛽∗) bt−1
(3.3.9.c) 𝑆𝑎𝑖𝑠𝑜𝑛: 𝑠𝑡 = γ(yt − lt−1 − bt−1) + (1 − γ)st−m
(3.3.9.d) 𝑃𝑟𝑜𝑔𝑛𝑜𝑠 : 𝑦̂𝑡+ℎ = 𝑙𝑡 + 𝑏𝑡 ℎ + 𝑠𝑡 +ℎ−𝑚(𝑘+1) , wobei k = ⌊(ℎ − 1)/𝑚⌋
Diese wird als Holt-Winters Methode bezeichnet, da die saisonale Komponente in die Prognosegleichung (3.3.9.d) einbezogen wird. Im Verhältnis zu Holts linearer Methode wird eine Zustandsgleichung für die Saison Komponente st ergänzt. Die saisonale Komponentengleichung wird wiederum aus einem gewichtete Durchschnitt aus der aktuellen Saisonkomponente (𝑦𝑡 − l𝑡−1 − 𝑏𝑡−1) und der gleichen Saisonkomponente des Vorjahres 𝑠𝑡−𝑚 gebildet. m beschreibt die Frequenz der Saisonalität . Für monatlic he Daten gilt demnach m = 12.
Aufbauend auf den Methoden von Brown, Holt und Winters wurden in der Folge weitere Methoden entwickelt, die Saison bzw. Trendkomponente auf unterschiedliche Weise in die Prognosemodelle integrieren. Von Gardner und McKenzie entwickelten eine Methode, die den linearen Trend über einen autoregressiven Parameter Φ abdämpfen kann.70 Der Parameter Φ kann insofern als „Persistenz“ des linearen Trends gedeutet werden.71 Hyndman et. al. nahmen schließlich 12 verschiedene Methoden der exponentiellen Glättung in Ihr „State Space Framework“ auf:
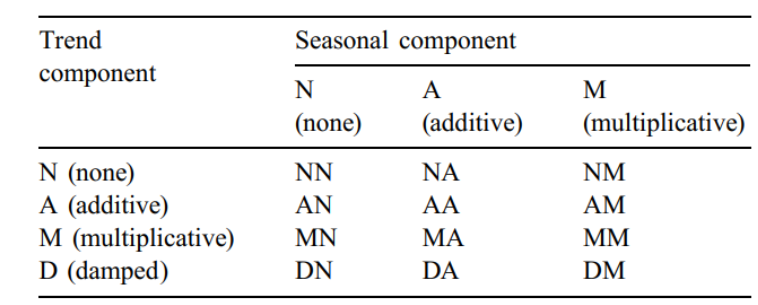
Für die Trendkomponente wird unterschieden ob sie additiv (A), multiplikativ (M), gedämpft (D) oder nicht (N) in die Methodengleichungen integriert wird. Für die Saisonkomponente werden die Ausprägungen „Nicht“ (N), „Additiv“ (A) und „Multiplikativ“ (M) unterschieden.
Insgesamt ergeben sich somit 12 Kombinationsmöglichkeiten an Methoden der exponentiellen Glättung. Die originäre Methode von Brown (3.3.4) enthielt weder Trendnoch Saisonkomponente und ist folglich in das Feld „NN“ der Abbildung 3 einzuordnen. Für Holts lineare Methode (Feld „AN“) wurde die Transformation in State Space Modelle gezeigt. Dabei wurde zwischen additiver und multiplikativer Integration des Fehlerterms ϵ𝑡 differenziert. In analoger Weise lassen sich sämtliche Methoden aus Abbildung 3 in multiplikative und additive State Space Modelle transformieren. Das State Space Framework wird auch als ETS-Framework bezeichnet, wobei das Akronym ETS nun als Abkürzung für „Error“, „Trend“ und „Season“ gedeutet werden kann. Insgesamt enthält das Framework folglich 2x4x3 Modellspezifikationen. In Anhang 1 sind die Gleichungen der klassischen Methoden, sowie die Modellgleichungen der State Space Modelle hinterlegt.

Recent Comments